Decision trees are desirable in that they scale well to larger datasets, they are robust against irrelevant features, and it is very easy to visualize the rationalization between a decision tree's predictions. Further, decision trees have low bias as there is minimal implicitly defined structure in the model (as opposed to linear regression, for example, which makes the assumption of linear relationships). Unfortunately, decision trees are prone to high variance and will overfit noisy data.
Random forests inherit the benefits of a decision tree model whilst improving upon the performance by reducing the variance. In building a random forest, we train a collection of decision trees on random subsets of the training data. Further, on each sampling from the population, we also sample a subset of features from the overall feature space. This adds randomness (with the intent to reduce variance in the end model) to the splitting process by limiting the features available for to split on for each individual base model.
Benefits of random sampling
As mentioned previously, one of the downsides of decision trees is the fact that the model behavior varies significantly dependent on which data was used for training. This can make it difficult to train a single model which generalizes well. This is visualized below in an example where the training data is a noisy estimate of the true data generating function, $f(x)$.
However, we can overcome this by training an ensemble of models, each trained on different subsets of our data. We'll observe this by training a collection of 50 trees, each trained on different random samples of $f(x)$ with a small amount of injected noise. Although each tree overfits to the sample on which it was trained, when you combine the predictions across trees you can build a much better estimate of the true data generating function.
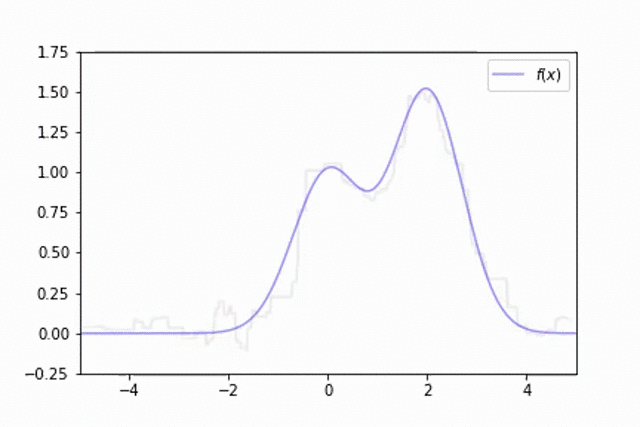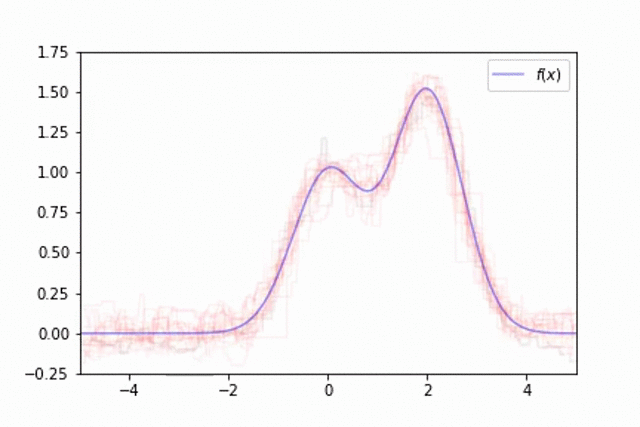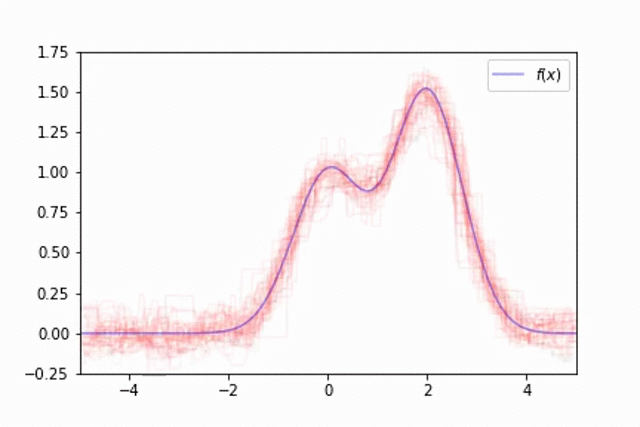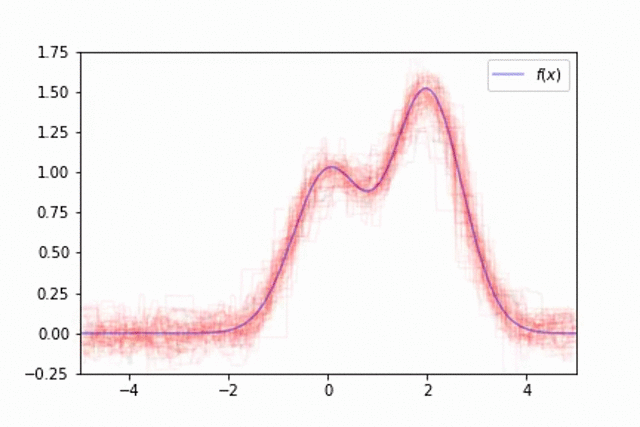
This technique of randomly sampling our data with replacement, training a base estimator, and then aggregating the individual predictions is known as bootstrap aggregating, or bagging for short.
As described earlier, when training a random forest we not only train each base estimator on a random subset of the training data, but also on a random subset of the features. This feature bagging ensures that each individual estimator splits on different aspects of the full observation, further reducing the variance of our predictions.
Empirical good default values are
max_features=n_featuresfor regression problems, andmax_features=sqrt(n_features)for classification tasks (wheren_featuresis the number of features in the data). – scikit-learn User Guide
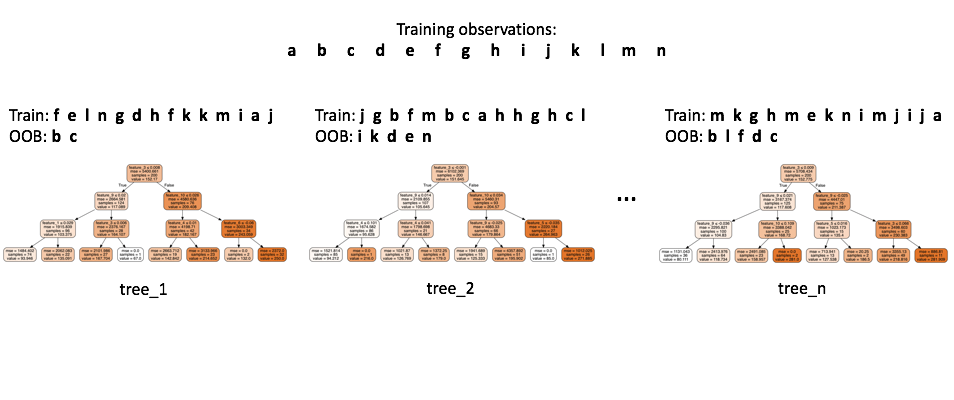
Out of bag score
When evaluating a machine learning model, we want to use independent data (not used during training) in order to form a good performance estimate. Typically, we do this by reserving a subset of our data for validation and never use it during training. However, because each individual tree only sees a random sample of data during training, we can build a performance estimate without the need for a separate hold-out set.
We do this by passing the training observations through only the subset of trees that never saw that data during training. This allows us to form an out of bag estimate of our model's performance.
